Tip: Open up YouTube, and adjust the speed to get through videos faster!
Homework:
Read Chapter 2 notes:
Watch some youtubes:
Lost of options to choose between:
TxTech:
Randall:
Yiheng:
Watch some youtubes:
Lost of options to choose between:
TxTech:
- Statics: Lesson 1- Intro and Newton's Laws, Scalars, and Vectors
- Statics: Lesson 2- Vector Language, Intro to Vector Addition
- Statics: Lesson 3-The Triangle Rule and Adding Vectors to find a Resultant
- Statics: Lesson 4- Vector Addition, Triangle Rule, and Cartesian and Vector Notation
- Statics: Lesson 5 - 2-D Find Resultant Vectors, Triangle Rule, Cartesian Components
- Statics: Lesson 6 - Finding Vector Components in Non-Orthagonal systems
- Statics: Lesson 7 - Most Missed topic in Statics, Cartesian Components
Randall:
Force vectors 1:
Force Vectors 2:
Yiheng:
Another statics resource:
Unit-1 Basics & Statics Of Particles (Resolution of Forces) - Engineering Mechanics
https://www.youtube.com/watch?v=4LTXVznGimwVectors:
https://ecourses.ou.edu/cgi-bin/display_lectures.cgi?course=st&status=disp_ch
If you find a better YouTube, post it in Ch2 for D2L points!

.
2.1-2.3: Vocabulary~~~~~~~~~~~~~~~~~~~~~~~
resultant force
- replacing multiple forces acting on a particle with a single equivalent force
- Make a parallelogram,
- resultant = diagonal of parallelogram
note: the magnitude of the vector
P + Q is NOT equal to the sum of the magnitudes of P+Q, you need to think about directions.
equilibrium
particle

force
Vector quantity
action of one body on another; characterized by:
- point of application
- magnitude
- SI units: 1,000N = 1 kN
- U.S. customary: 1,000 lb = 1 kip
- Direction of Force
- line of action - line force acts along
- sense: arrow pointing which way it is acting; ↑? ↓?
Scalar
- has magnitude but not direction.
- Examples:
- mass,
- volume,
- temperature
Vector
- has magnitude and direction
- add according to the parallelogram law.
- Examples:
- displacements
- velocities
- accelerations
Vector classifications
- Fixed or bound vectors
- Free vectors
- Sliding vectors
2.4 Addition of vectors ~~~~~~~~~~~~~~~~~~~~~~~~
Trapezoid rule for vector addition
Trapezoid rule for vector addition
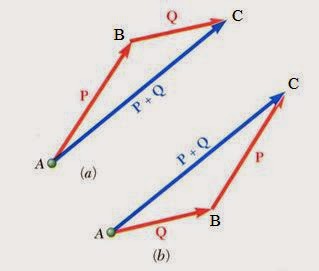
Triangle rule for vector addition
- Just draw half of the parallelogram
- arrange vectors head to tail
- Just draw half of the parallelogram
- arrange vectors head to tail
Sum of three or more vectors
Add two together, and then add on the third etc.
P + Q + S = (P + Q) + S

It doesn't matter what order you add them
Product of a Scalar and a Vector
- Keep the same line of action
- Change the magnitude
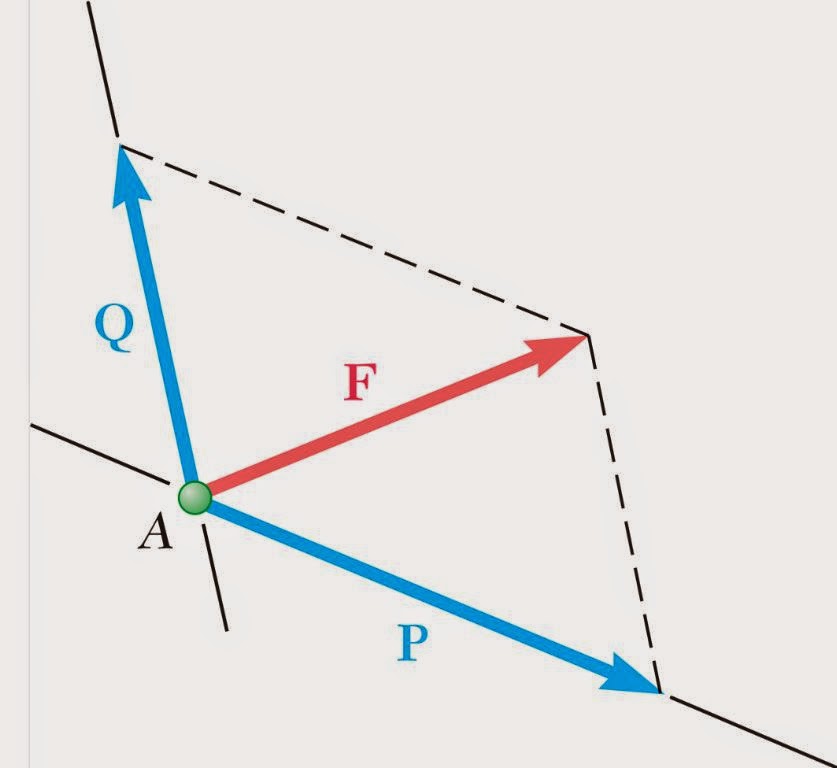
concurrent forces
all forces pass through a common point
Resultant of concurrent forces:
Replace multiple forces with single force,
.
R → same effect as S+P+Q on "A"
Resolution of a force into components
Describe force in terms of x, y, z
Trig Review~~~~~~~~~~~~~~~~~~~~~~~~~~.
Law of cosines
Law of sines
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
..


















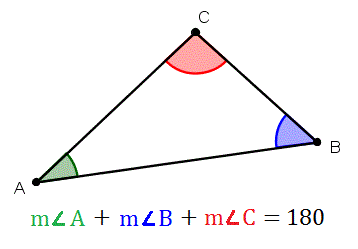
No comments:
Post a Comment